Warning: This is a preliminary version, more exercises may be added soon, so come back to this page soon!.

In addition to all concepts from Test 1, and Test 2

You should be able to define or explain the following terms:

• Queue ADT and operations
• Dictionary ADT and operations
• Binary tree
• Tree traversals: pre-order, in-order, post-order, and level-order traversals
• Binary search trees and the BST property

You should also have a good understanding of how elements are inserted and removed from a BST.

Practice problems

1. For each data structure and implementation covered in the course, come up with a real-world application that motivates the data structure. The data structure should be able to provide a more efficient solution or simpler to the problem then any other structure covered at that point in the course.


2. (hard) Give a binary tree with integer keys in its nodes, whose traversals are:
   • PreOrder: [80 46 92 90 121 111 105]
   • InOrder: [46 80 90 92 105 111 121]
   • PostOrder: [46 90 105 111 121 92 80]
   Is the tree a BST? Justify your response.


3. Consider the following tree:
   
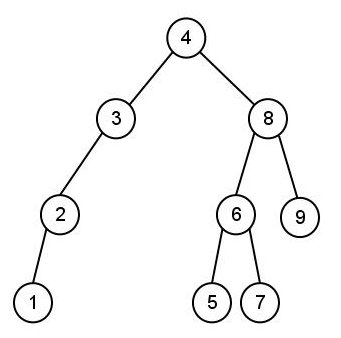
   1. What is the pre-order traversal of the tree?
   2. What is the in-order traversal of the tree?
   3. What is the post-order traversal of the tree?
   4. What is the level-order traversal of the tree?
   5. Identify if it is a tree, binary tree, binary search tree
   6. Based on your previous answer, draw the tree obtained by inserting 10 into the tree.
   7. Draw the tree obtained by deleting 2 from the tree.
   8. Draw both trees that might be obtained by deleting 4


4. Using the IntBST header files in the fromClass section, draw a stack diagram at the point indicated by a comment in the following code. You can assume that the inserts are made using the code I showed in class.

   int main() {
   IntBST *dict = new IntBST();
     dict->insert(5, 5);
     dict->insert(9, 9);
     dict->insert(11, 11);
   
     // draw a stack diagram here
   
     dict->insert(10, 10);
   
     cout << "goodbye!" << endl;
   }
   			

5. Try to follow the sequence of recursive calls that will be made by doing the last insert in the code of the previous section. Try to trace exactly how each pointers in the structure are updated.
6. In class, we defined a Queue using various List implementations. Let's flip this around. Consider the following (somewhat strange) List definition, QueueIntList, that uses an awesomely cool MagicIntQueue to represent the data in the list. (Note that the details of MagicIntQueue are not given, but are also unnecessary given what you know about interfaces.)

   #ifndef STUDYGUIDE_QUEUEINTLIST_H
   #define STUDYGUIDE_QUEUEINTLIST_H
   
   #include "list.h"
   #include "magicIntQueue.h"
   
   class QueueIntList : public List<T> {
   protected:
      MagicIntQueue values;
   
   public:
      QueueIntList();
      ~QueueIntList();
      void insertAtHead(int item);
      void insertAtTail(int item);
      int getSize();
      bool isEmpty();
      // ...etc. all List methods are declared here
   };
   
   #endif //STUDYGUIDE_QUEUEINTLIST_H
   

   Using the above declarations, complete an implementation for the methods getSize(), insertAtHead(T item), and removeTail(). Your answers should be written as they would appear in queueList.cpp Again, the details of MagicQueue are not important; you should assume it implements a Queue interface properly.

Home Page